こちらを読むと
- scikit-learnのload_iris datasetのデータ観察の初歩が分かります。
- 特に散布図マトリクス(scatter_matrix)の解説をします。
- 記事の所要時間は15分です。
前回のブログで、load_irisのdatasetを解説しました。
今回はこのデータを観察していきます。
データ観察のソースコード
一番最後のコードは散布図マトリクス(scatter_matrix)を表しています。こちらは初見だとよくわからないと思うので、特に解説していきます。
散布図マトリクスの解説
横軸と縦軸、それぞれに、特徴量が並びます。
横軸は左から、がくの長さ/額の幅/花びらの長さ/花びらの幅、の順番です。
縦軸は上から、がくの長さ/額の幅/花びらの長さ/花びらの幅、の順番です。
そうなると、例えば一番左下のセルは、がくの長さ-花びらの幅の組み合わせになり、その2つをそれぞれ横軸、縦軸にとった散布図が表示されます。
マトリクスの対角方向に対称なセルは、横軸と縦軸の向きが変わるだけで同じ組み合わせなので、横と縦の方向をひっくり返したような形になっています。
実質は同じ情報を表しています。
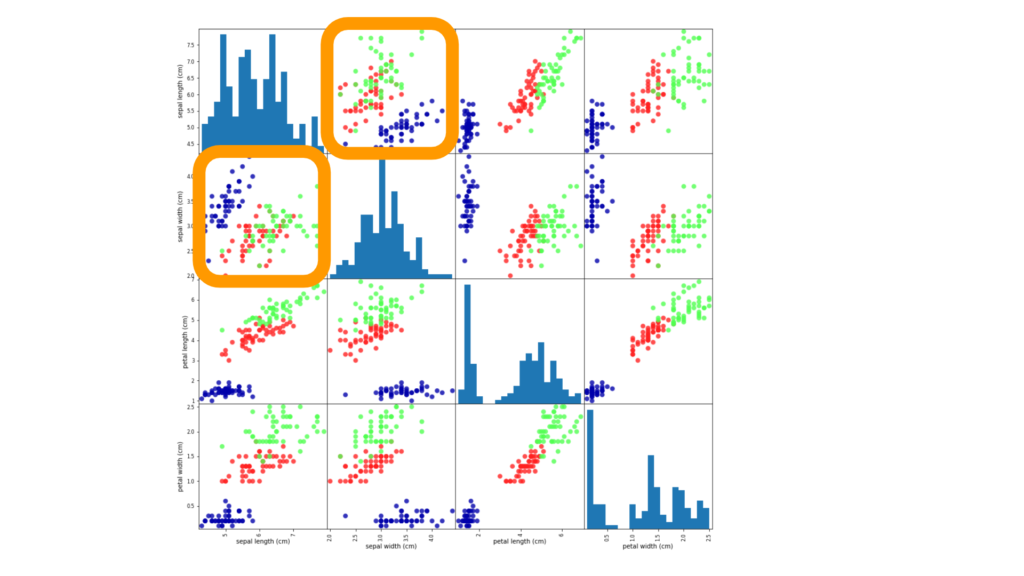
マトリクスの対角方向に対称なセルは 同じ情報を表す
横軸と縦軸が同じ特徴量となるセル、例えば、がくの長さ-がくの長さの組み合わせのセルは、散布図を描いても意味がないため、代わりにヒストグラムが表示されます。
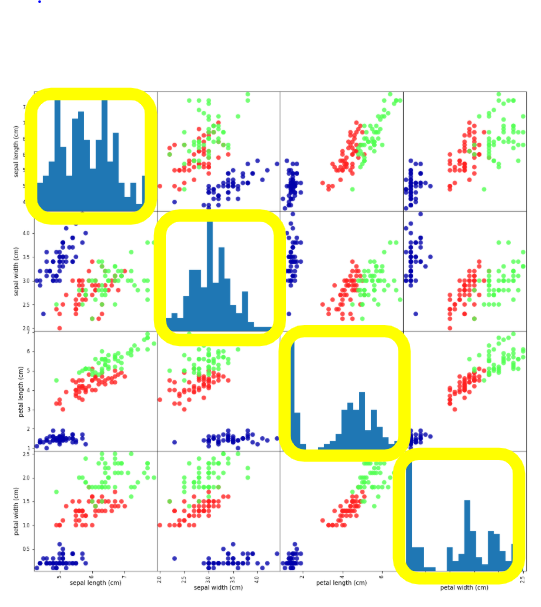
ヒストグラムが表示される
散布図の解説
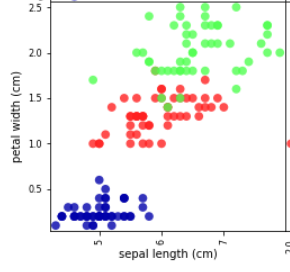
例えばがくの長さ-花びらの幅の組み合わせだと、以下のような散布図になっています。
1点が1つのアヤメのデータを表しています。
ある1つのアヤメについて、がくの長さと花びらの幅によって、散布図のどの位置にプロットするかが決まり、アヤメの種類によって色が決まります。

この散布図は、青/赤/緑が、わりときれいに分かれているので、がくの長さと花びらの幅の組み合わせは、アヤメの分類に使えそうだと判断できるわけです。
では以下の、がくの長さ-がくの幅の組み合わせはどうでしょうか。
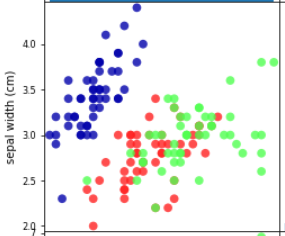
青色のアヤメはきれいに分かれていますが、赤と緑はきれいに分かれているとは言い難いです。
したがって、この特徴量の組み合わせでは分類に使えない可能性があるため、どちらかの特徴量を使わない方が良いかもしれない、という検討ができるわけですね。
まとめ
- scikit-learnのload_iris datasetのデータ観察の初歩が分かりました。
- 特に散布図マトリクス(scatter_matrix)の解説をしました。
機械学習のモデルを作成する前に、データの分析は必須ですが、散布図マトリクスは道具の一つとして使えそうですね。
こういうデータの分析に使える武器を増やしていけば、使用するデータの取捨選択の質を上げることができそうです!
Reference
Pythonではじめる機械学習
https://www.oreilly.co.jp/books/9784873117980/