ロジスティック回帰①

こちらを読むと

• 機械学習のロジスティック回帰の概要を知ることができます
• ロジスティック回帰のモデル式が分かります

ロジスティック回帰とは

分類問題に使われる機械学習のモデルです。
単純パーセプトロンのように、”0 or 1″ではなく、
“0の確率は〇%、1の確率は△%”のように、出力を確率で表すことができます。

何が嬉しいか

　ロジスティック回帰で出力を確率で表せると何が嬉しいかというと、
モデルを使う人が、グレーゾーンの結果をどうするか、決められることです。
詳解ディープラーニングやCourseraの機械学習コースでも挙げられていますが、スパムメールの分類を行う際の例を挙げます。
　スパムメールか、通常メールか、の分類をするとき、今までの学習結果を用いても、”スパム or 通常”とはっきり分けられることはなく、どうしてもグレーゾーンが存在します。例えば、100%ではないけれど、56%の確率でスパムメールと判断される場合などです。
　開発システムの仕様として、40%以上でスパムメールと判断された場合は、警告を出す、と決めることはできます。それが現場によって、30%だったり、60%だったりすることもあるでしょう。
　すなわち、”0 or 1″ではなく、その中間（グレーゾーン）も分かるので、モデルを使う人が結果に応じて処理を決めることができます。

シグモイド関数

ロジスティック回帰には、出力にシグモイド関数を使います。シグモイド関数の式は以下の形です。

$$
\sigma(x) = \frac{1}{1+e^{-x}}
$$

シグモイド関数がロジスティック回帰に用いられるのは、以下の2点の理由によるものです。

1. 出力が0～1の間で出力される
2. 微分計算の結果をシグモイド関数で表せる

2の微分計算の結果は、以下のようになっており、微分計算結果がさらにシグモイド関数で表せます。この特長が、非常に都合がよいのです。

$$
\sigma'(x) = \sigma(x)(1 – \sigma(x))
$$

モデル式

ある入力\({\bf x}\)に対して、ニューロンが発火するかしないかをとり得る確率変数を\(C\)とおきます。すなわち\(C\)は、ニューロンが発火する場合\(C\)=1、発火しない場合\(C\)=0です。単純パーセプトロンと同様に、以下のようなモデルを考えた場合、

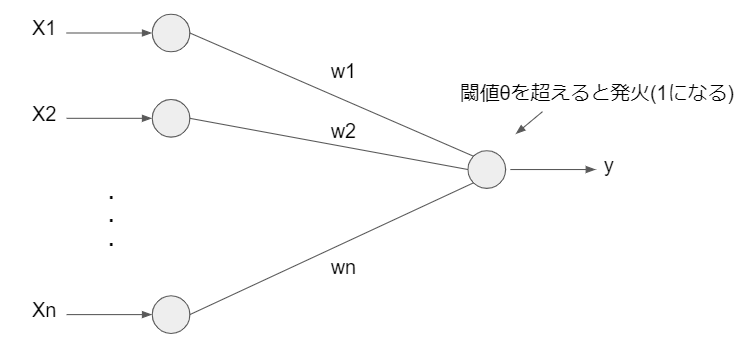
ニューロンが発火する確率は

$$
p(C = 1 | {\bf x}) = \sigma({\bf w}^T{\bf x} + b)
$$

となります。確率は和が1なので、ニューロンが発火しない確率は

$$
p(C = 0 | {\bf x}) = 1-p(C = 1 | {\bf x})
$$

となります。ここで、\(y:=\sigma({\bf w}^T{\bf x} + b)\)とおくと、上記の2式は以下のようにひとまとめにできます。

$$
p(C = t | {\bf x}) = y^t(1 – y)^{1-t}
$$

この式変形は、ちょっとわかりにくいのですが、t=0、t=1をそれぞれ代入したとき、元の式になることが分かるかと思います。

まとめ

• 機械学習のロジスティック回帰の概要を知ることができました
• ロジスティック回帰のモデル式が分かりました

次回はこのモデル式から、どのように学習を行っていくかについて説明します。
ロジスティック回帰もニューラルネットワークの基本になるので、しっかり理解していきたいところです！

Reference

詳解ディープラーニング
https://book.mynavi.jp/manatee/books/detail/id=72424