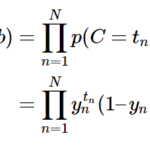こちらを読むと
- 単純パーセプトロンの実装方法が分かります
数式おさらい
前回のブログで、単純パーセプトロンのモデル式および、重みとバイアスの更新式を以下のように定義できました。
$$
y = f({\bf w}^T{\bf x} + b)
$$
$$
\begin{eqnarray}
\Delta{\bf w}&=&(t-y){\bf x} \\
\Delta b&=&(t-y)
\end{eqnarray}
$$
$$
\begin{eqnarray}
{\bf w}^{(k+1)}&=&{\bf w}^{(k)}+\Delta{\bf w} \\
b^{(k+1)}&=&b^{(k)}+\Delta b
\end{eqnarray}
$$
実装
ここからは実装です。
プログラムは、詳解ディープラーニングを参考にさせていただきました。
まとめ
- 単純パーセプトロンの実装方法が分かりました
ここまで、単純パーセプトロンについて、
理論→数式化→実装
と進めてきました。ほかのアルゴリズムでも、同じ方法で研究してみると理解しやすいと思います。
Reference
詳解ディープラーニング
https://book.mynavi.jp/manatee/books/detail/id=72424