こちらを読むと
- 単純パーセプトロンのモデルの数式での表し方が分かります
モデルの数式
前回のブログで、以下のような\(f(x)\)を定義すると、
$$
\begin{eqnarray}
f(x)=\left\{ \begin{array}{ll}
1 & (x \geq 0) \\
0 & (x < 0 ) \\
\end{array} \right.
\end{eqnarray}
$$
単純パーセプトロンのモデルは以下の式で表せると説明しました。
$$
y = f(w_1x_1+w_2x_2 +\cdots+w_nx_n -\theta)
$$
ここからさらに踏み込んで、以下のように置くと、
$$
\begin{equation}
{\bf x}=
\begin{pmatrix}
x_{1} \\
x_{2} \\
\vdots \\
x_{n}
\end{pmatrix}
{\bf w}=
\begin{pmatrix}
w_{1} \\
w_{2} \\
\vdots \\
w_{n}
\end{pmatrix}
\end{equation}
$$
モデルの出力は
$$
y = f({\bf w}^T{\bf x} + b)
$$
と表すことができます。
この式が、単純パーセプトロンのモデル式です。
誤り訂正学習法の更新式
正解の出力を\(t\)としモデルの出力を\(y\)とすると、誤り訂正学習法という方法で、以下のように重みとバイアスの訂正量を表すことができます。
$$
\begin{eqnarray}
\Delta{\bf w}&=&(t-y){\bf x} \\
\Delta b&=&(t-y)
\end{eqnarray}
$$
こいつの解釈は、感覚的になってしまうのですが、
バイアス\(b\)は単純に\(t\)と\(y\)の差を埋めればよいため、\(t-y\)とし、
重み\(w\)は、\(x=0\)ならば、更新しても意味がないため、\(t-y\)に\(x\)を掛けている(\(x=0\)ならば0になる)ということだと思っています。
以上から、重みとバイアスの更新式は以下のようになります
$$
\begin{eqnarray}
{\bf w}^{(k+1)}&=&{\bf w}^{(k)}+\Delta{\bf w} \\
b^{(k+1)}&=&b^{(k)}+\Delta b
\end{eqnarray}
$$
まとめ
- 単純パーセプトロンのモデルの数式での表し方が分かりました
単純パーセプトロンはディープラーニング分野の基礎中の基礎なので、ディープラーニングを学習したい方は、間違いなく押さえておくべきです!
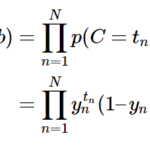





[…] 次回は、上記の式変形を行い、ベクトル形式での式表示、および誤り訂正学習法の方法について説明します。 […]