こちらを読むと
- ニューラルネットワークのパーセプトロンの概要を知ることができます
単純パーセプトロンとは
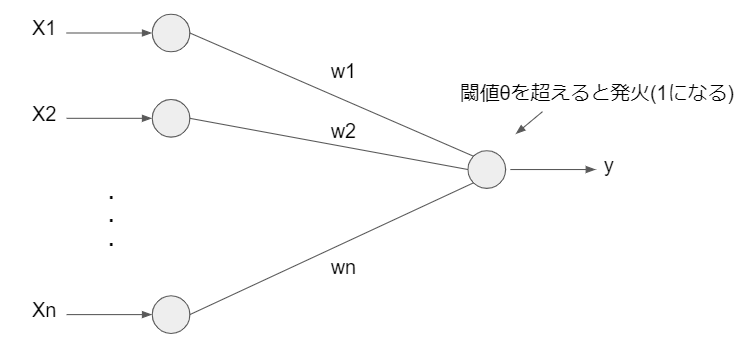
ニューラルネットワークの1種で、以下のような入力Xに重みwをかけて加算し、
出力yを取り出すネットワークです。
式
上記の図を式で表すと、以下のようになります。
$$
\begin{eqnarray}
y=\left\{ \begin{array}{ll}
1 & (w_1x_1+w_2x_2 +\cdots+w_nx_n \geq \theta) \\
0 & (w_1x_1+w_2x_2 +\cdots+w_nx_n < \theta) \\
\end{array} \right.
\end{eqnarray}
$$
ここで、以下のような関数を考えます。
$$
\begin{eqnarray}
f(x)=\left\{ \begin{array}{ll}
1 & (x \geq 0) \\
0 & (x < 0 ) \\
\end{array} \right.
\end{eqnarray}
$$
すると、ネットワークの出力yの式は、以下のように書き直すことができます。
$$
y = f(w_1x_1+w_2x_2 +\cdots+w_nx_n -\theta)
$$
まとめ
- ニューラルネットワークのパーセプトロンの概要を知ることができました
次回は、上記の式変形を行い、ベクトル形式での式表示、および誤り訂正学習法の方法について説明します。
Reference
詳解ディープラーニング
https://book.mynavi.jp/manatee/books/detail/id=72424

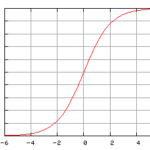
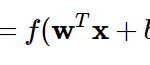






[…] 前回のブログで、以下のような\(f(x)\)を定義すると、 […]