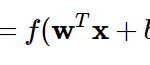こちらを読むと
- 多クラスロジスティック回帰のソフトマックス関数の微分 の導出過程が分かります。
前回の記事で、ソフトマックス関数の微分の導出過程を途中まで記載しました。今回はその続きです。
前回のおさらい
入力を\(x_i\)、出力を\(y_i\) (\(i\)=1,2, …n)とすると、
$$
\begin{pmatrix}
y_1 \\
y_2 \\
\vdots \\
y_n
\end{pmatrix}
=
\frac{1}{\sum_{j=1}^n e^{x_j}}
\begin{pmatrix}
e^{x_1} \\
e^{x_2} \\
\vdots \\
e^{x_n}
\end{pmatrix}
$$
以下のようにおくと、
$$
Z := \sum_{j=1}^n e^{x_j}
$$
\(i=j\)のとき、ソフトマックス関数の微分は、
$$
\begin{eqnarray}
\frac{\partial y_i }{\partial x_i} &=& \frac{e^{x_i}Z – e^{x_i}e^{x_i}}{Z^2} \\
&=& \frac{e^{x_i}}{Z}-(\frac{e^{x_i}}{Z})^2= y_i(1 – y_i)
\end{eqnarray}
$$
となると説明しました。
今回は、\(i \neq j\)の場合について説明します。
ソフトマックス関数の微分(続き)
\(i \neq j\)の場合、
$$
\begin{eqnarray}
\frac{\partial y_i}{\partial x_j}&=&\frac{\partial}{\partial x_j} \frac{e^{x_i}}{Z}\\
&=& \frac{1}{Z^2}( \frac{\partial e^{x_i}}{\partial x_j}Z – e^{x_i}\frac{\partial Z}{\partial x_j} )\\
&=& \frac{1}{Z^2}( -e^{x_i}\frac{\partial Z}{\partial x_j} ) (※1)\\
&=& \frac{1}{Z^2}( -e^{x_i}\frac{\partial}{\partial x_j}(e^{x_1} + e^{x_2} + \dots + e^{x_j} + \dots + e^{x_n}) ) \\
&=& \frac{-e^{x_i}e^{x_j}}{Z^2} \\
&=& -y_iy_j
\end{eqnarray}
$$
(※1) $$\frac{\partial e^{x_i}}{\partial x_j}=0より (x_iの関数をx_jで微分するため)$$
いままでの式をまとめると、以下で表すことができます。
$$
\frac{\partial y_i}{\partial x_j} =
\begin{cases}
y_i(1 – yi)~~~(i = j) \\
-y_iy_j~~~~~~~~(i \neq j)
\end{cases}
$$
まとめ
- 多クラスロジスティック回帰のソフトマック関数の微分を説明しました。
ここまでで、ようやくモデル式を表すための準備ができました。次回はモデル式の導出に入っていきます。
Reference
詳解ディープラーニング
https://book.mynavi.jp/manatee/books/detail/id=7242