こちらを読むと
- 多クラスロジスティック回帰のソフトマックス関数の微分の導出過程が分かります。
前回の記事で、多クラスロジスティック回帰の概要を説明しました。今回は、モデル式の導出まで行い、最適解を求める下準備をしたいと思います。
ソフトマックス関数のおさらい
ソフトマックス関数は、多クラス分類を可能にする式で、n次元ベクトル\({\bf x}\)に対して以下のように表されるのでした。
$$
softmax({\bf x})_i = \frac{e^{x_i}}{\sum_{j=1}^n e^{x_j}} (i=1,2,…,n)
$$
ここで気を付けてほしいのが、分子と分母の\(x\)の添え字が異なっている点です。分子は\(i\)で、1つの項目を表しているものです。この関数自体の添え字ということでしょうか。分母は\(j\)で、全体の総和に使っているものです。\(j\)=1~nまで加算するときの一時変数ですね。
ちなみに私は、最初この2つの区別がついていなくて、式の理解をするのに1時間くらいかけてしまいました 笑。
ソフトマックス関数は、数式を見てもらうとわかりますが、「それ / 全体」を表しており、入力が\(x_i\)のときに出力が発火する確率を表しています。なぜ入力をのものの\(x\)ではなく、\(e^x\)を使うかは、「発火する」「発火しない」の差を明確にするためです。\(x\)が大きくなるにつれ、\(e^x\)はより大きくなります。
ソフトマックス関数の微分
入力を\(x_i\)、出力を\(y_i\) (\(i\)=1,2, …n)とすると、
$$
\begin{pmatrix}
y_1 \\
y_2 \\
\vdots \\
y_n
\end{pmatrix}
=
\frac{1}{\sum_{j=1}^n e^{x_j}}
\begin{pmatrix}
e^{x_1} \\
e^{x_2} \\
\vdots \\
e^{x_n}
\end{pmatrix}
$$
と表せます。またさらに右辺の分母を
$$
Z := \sum_{j=1}^n e^{x_j}
$$
とおいたとき、ソフトマックス関数の微分を求めると、まず\(i\)=\(j\)では
$$
\frac{\partial y_i }{\partial x_i} = \frac{e^{x_i}Z – e^{x_i}e^{x_i}}{Z^2} = y_i(1 – y_i)
$$
となり、\(i\)≠\(j\)では
$$
-y_iy_j
$$
となります。
この式変換が分かりにくいので、次回はもう少し詳細に説明したいと思います。
まとめ
- 多クラスロジスティック回帰のモデル式のソフトマックス関数の微分を途中まで説明しました。
Reference
詳解ディープラーニング
https://book.mynavi.jp/manatee/books/detail/id=72424
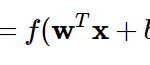



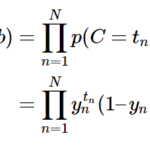





[…] 前回の記事で、多クラスロジスティック回帰のモデル式の導出過程を途中まで記載しました。今回はその続きです。 […]