
こちらを読むと
- Pythonでの統計検定方法の例が分かります
- 二項分布を用いた検定の方法が分かります
やりたいこと
先日作成した以下のサイコロを用いて、このサイコロが普通のサイコロかどうかを調べたいと思います。
サイコロの仕様:
1:1/24の確率で出る
6:7/24の確率で出る
2~5:それぞれ1/6の確率で出る
調べる方法
1の目に着目すると、サイコロを投げて、(1が出る, 1が出ない)という2種類の結果が得られるため、この試行は”二項分布”という分布に従います。以下の手順で、普通のサイコロかどうかを調べることができます。
- サイコロを12000回投げ、1の目が出る確率を調べる。
- 仮説を立てる。帰無仮説:サイコロを振って1の目が出るのは2000回(確率1/6なので普通のサイコロ)、対立仮説:サイコロを振って1の目が出るのは2000回でない(普通のサイコロでない)
- 有意水準αを設定する。α=0.05とする。
- 検定統計量を決める。二項分布では、X=「1が出た回数」、p=「1が出る確率」、n=「試行回数」とすると、統計量zは以下の式①で表される。
- 棄却ルールを決める。95%の確率で帰無仮説が成り立つことを考えると、zが±1.96を超えれば、帰無仮説を棄却する(普通のサイコロではない)。
- 検定統計量をもとに結論を出す。
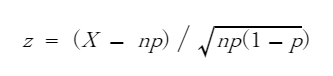
サイコロを12000回投げる
サイコロを12000回投げる試行を行うプログラムは、以下のようになります。
count = {1:0, 2:0, 3:0, 4:0, 5:0, 6:0}
for i in range(0,12000):
dice = get_dice()
count[dice] += 1
その結果は以下のようになりました。
1の目が少ないですね。ただし、この結果が本当に普通でないのか、検定を行って確実なものにします。
|
1 |
{1: 509, 2: 2019, 3: 1941, 4: 2035, 5: 1994, 6: 3502} |
検定を行う
式①を用いて統計量zを求めると、以下のようになります。
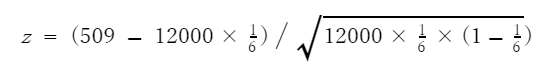
結果は、z=-36.521…となり、-1.96を大幅に超えていました。
したがって、帰無仮説: サイコロを振って1の目が出るのは2000回(確率1/6なので普通のサイコロ)は棄却され、このサイコロは普通ではないイカサマサイコロであることが分かります。
ちなみに、通常通り1/6の確率で目が出る2の目で試すと、
z=0.465…となり、±1.96に収まっていることが分かります。
まとめ
- Pythonでの統計検定方法の例が分かりました
- 二項分布を用いた検定の方法が分かりました
検定を行うときは、具体的な試行で試すとわかりやすいと思います!








