
こちらを読むと
- 多クラスロジスティック回帰のモデル式の概要と導出方法が分かります。
モデルのおさらい
多クラスロジスティック回帰のモデルは、以下のようになっていました。
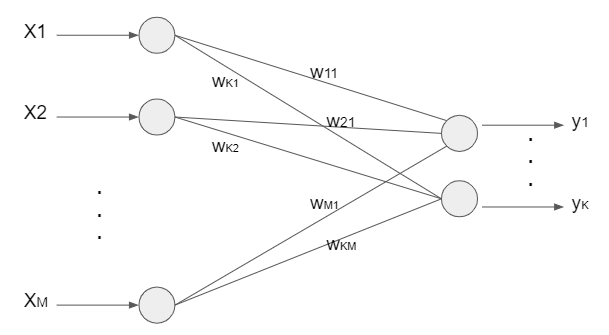
モデル出力式の導出(代表値)
上記のモデルから、出力式は
$$
{\bf y} =
\begin{pmatrix}
y_1 \\
y_2 \\
\vdots \\
y_k \\
\vdots \\
y_K
\end{pmatrix}
$$
となります。
2値ロジスティック回帰と同じように、入力\(x_m\)、重み\(w_{km}\)、バイアス\(b_k\)を使って、出力を以下のように表すことができます。
$$
\begin{eqnarray}
y_k &=& f(w_{k1}x_1 + w_{k2}x2 + \dots + w_{kM}x_M + b_k)\\
&=& f({\bf w}_k^T{\bf x + b_k}) ※1
\end{eqnarray}
$$
※1 以下のようにおいた場合
$$
{\bf w_k} =
\begin{pmatrix}
w_{k1}\\
w_{k2}\\
\vdots\\
w_{kM}
\end{pmatrix}
{\bf x} =
\begin{pmatrix}
x_1\\
x_2\\
\vdots\\
x_M\\
\end{pmatrix}
$$
2値ロジスティック回帰と同じような式の形にすることができました。
モデル出力式の導出(全体)
ここまでは出力の代表値\(y_k\)の式を求めました。
出力の全体\({\bf y}\)に対する式はどうなるでしょうか。
目標としては、単純パーセプトロンや2値ロジスティック回帰の式
$$
y = f({\bf w}^T{\bf x} + b)
$$
の形を目指したいです。
そのために、以下のようにおきます。
$$
\begin{eqnarray}
W &=& ({\bf w}_1 \dots {\bf w}_k \dots {\bf w}_K)^T\\
&=&
\begin{pmatrix}
w_{11} \dots w_{1n} \dots w_{1M}\\
\vdots \hspace{30pt} \vdots \hspace{30pt} \vdots\\
w_{k1} \dots w_{kn} \dots w_{kM}\\
\vdots \hspace{30pt} \vdots \hspace{30pt} \vdots\\
w_{K1} \dots w_{Kn} \dots w_{KM}
\end{pmatrix}
\end{eqnarray}
$$
$$
{\bf b} =
\begin{pmatrix}
b_1\\
\vdots\\
b_k\\
\vdots\\
b_K
\end{pmatrix}
$$
こうすれば、モデル出力式を以下のように表せます。
$$
{\bf y} = f(W{\bf x} + {\bf b})
$$
まとめ
- 多クラスロジスティック回帰のモデル式の概要と導出方法が分かりました。
多クラスになったとしても、ベクトルや行列をうまく使えば、シンプルな式で表現できるのはすごいことだと思いませんか?
次回は、誤差関数を求めていきます。
Reference
詳解ディープラーニング
https://book.mynavi.jp/manatee/books/detail/id=72424







[…] 前回までの記事で、多クラスロジスティック回帰のモデル出力がの式で表せることを説明しました。 […]